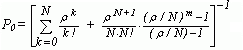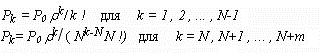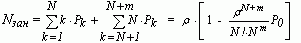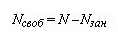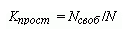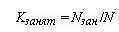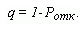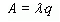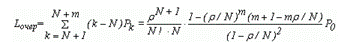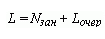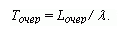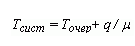Линейное программирование

Линейное программирование представляет собой математический метод для принятия решений, заключающийся в поиске оптимального значения целевой функции, зависящей от некоторых переменных, при заданных дополнительных ограничениях. При этом и целевая функция и ограничения должны быть линейны. Существуют математические алгоритмы и программное обеспечение, позволяющее искать оптимум целевой функции при заданных ограничениях. Очевидно, что найденные значения переменных функции, соответствующие ее оптимуму и будут являться искомым решением.

Для примера рассмотрим простую задачу, которую решим графически.

Пусть перед компанией А стоит задача организовать рекламную компанию, длительностью один месяц, на которую выделено в бюджете 10.000$. Имеется возможность разместить рекламный ролик на радио (стоимость минуты эфирно времени на радио 500$) и/или на телевидении (стоимость минуты на местном TV равна 1000$). Имеются статические данные об эффективности маркетинговых каналов. Так 1 минута на телевидении в среднем обеспечивает рекламодателю 15 новых клиентов, а 1 минута на радио – 10 новых клиентов. Кроме того, все рекламодатели должны соблюдать местное антимонопольное законодательство, в рамках которого общая длительность транслированных по всем каналам рекламных роликов не должна превышать 15 минут в месяц.

Вопрос: каким образом максимально эффективно (по количеству новых клиентов) с учетом бюджетного и законодательного ограничения распределить рекламную кампанию между радио и ТВ?

Для принятия решения в данной ситуации воспользуемся методом линейного программирования. Пусть X – общая продолжительность роликов на радио (в минутах), а Y – на ТВ. Тогда целевая функция (эффективность = кол-во новых клиентов от кампании) будет представлять из себя:

F(X,Y) = 10*X + 15*Y

Ограничения:

500*X + 1000*Y <= 10.000 (бюджетное)

X + Y <= 15 (законодательное)

X >= 0, Y >= 0 (очевидное)

Теперь изобразим имеющиеся ограничения графически.

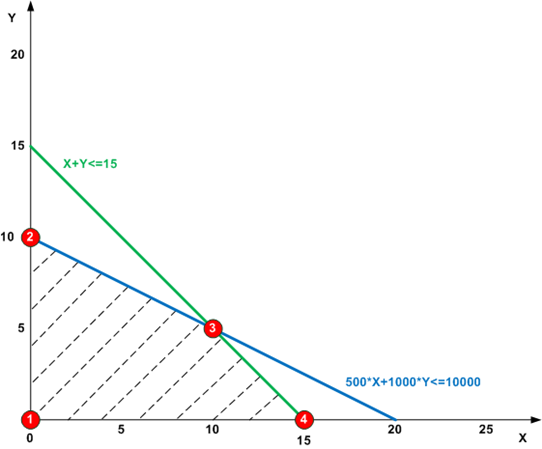
Многоугольник, с вершинами 1, 2, 3 и 4 представляет из себя множество возможных значений X и Y, удовлетворяющих заданным ограничениям (заштрихованная область).

Теперь задача сводится к поиску оптимума целевой функции F(X,Y) на данном множестве допустимых значений переменных. Теорема, лежащая в основе линейного программирования, гласит, что максимум линейной функции на выпуклом многоугольнике (или выпуклом многограннике, если переменных больше двух) достигается в вершинах этого многоугольника (многогранника). Поэтому, для того, чтобы найти оптимальные значения X и Y в нашем случае достаточно рассчитать значения целевой функции в четырех вершинах полученного многоугольника и выбрать из них максимальное (оптимальное). Соответствующие данному значению целевой функции значения X и Y и будут решением.

Рассчитаем значения F(X,Y) в точках 1-4.

Как видим, максимальное значение новых клиентов (175) достигается при условии размещения роликов на радио с общей длительностью 10 минут и на ТВ с общей длительностью 5 минут.

Календарно-сетевое планирование

Календарно-сетевое планирование позволяет применить математический аппарат теории графов для решения задач управления проектами. Проект может быть представлен в виде последовательности взаимосвязанных работ, каждая из которых имеет определенную длительность и может характеризоваться дополнительными параметрами (стоимость, требуемые ресурсы и др.). В рамках данного определения проект может быть изображен в виде сетевого графика, как показано ниже. На нем в узлах показаны работы, составляющие проект. Дуги представляют собой события, инициирующие переходы к последующим работам проекта.

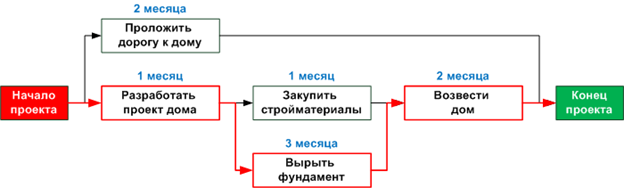
Красным на сетевом графике выделен критический путь, который представляет собой самый длинный «маршрут» от начала проекта до его окончания. Любая задержка в работах, составляющих критический путь, приведет к задержке всего проекта в целом.

Работы, не лежащие на критическом пути, имеют запас времени на завершение. В нашем примере работа «Проложить дорогу к дому» имеет запас времени 4 месяца, а работа «Закупить стройматерилы» — 2 месяца.

Наряду с сетевым графиком для принятия решений в области управления проектами используется линейная диаграмма (или ее разновидность, на которой также обозначены взаимосвязи между работами – диаграмма Ганта).

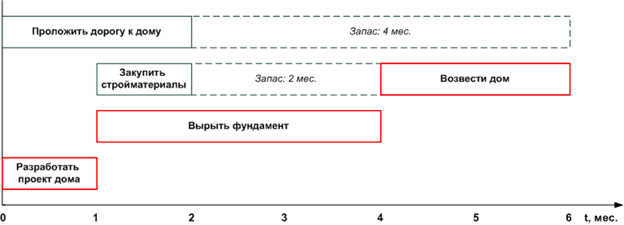
На линейной диаграмме наглядно видны возможности для изменения сроков начала и завершения работ. Например, если несколько запараллеленных работ требуют общего ресурса, то при наличии запасов их можно разнести во времени. В нашем случае во второй месяц строительства у прораба на проекте могут возникнуть сложности с одновременным техническим руководством строительством дороги, закупкой стройматериалов и рытьем фундамента. Поэтому, например, можно принять решение о переносе строительства дороги на более поздний период – 3-й и 4-й месяцы, когда закупка материалов будет завершена, а работы по рытью фундамента будут отработаны за первый месяц их выполнения и прораб сможет параллельно заниматься дорогой.

Также математический аппарат теории графов часто применяется для решения оптимизационных задач при управлении проектами. Например, если для каждой работы задать функции, определяющие зависимость ее стоимости от продолжительности выполнения, то методами линейного программирования можно рассчитать оптимальные длительности работ проекта (и, соответственно, даты их начала и завершения), обеспечивающие минимальную стоимость проекта в определенных временных рамках.

Теория игр

Теория игр занимается изучением т.н. «конфликтных» ситуаций, где сталкиваются интересы двух или более сторон: индивидов, конкурирующих организаций, партий и др. При этом каждая сторона сталкивается с проблемой принятия решений по выбору для себя оптимальной стратегии поведения в этой «игре», направленной на максимизацию выигрыша или минимизацию проигрыша. Для решения этой задачи в рамках теории игр существует аналитический и математический аппарат, позволяющий наглядно описать «правила игры» и возможные стратегии поведения игроков, а также определить оптимальную из этих стратегий.

Рассмотрим применение элементов теории игр на примере т.н. дилеммы заключенных. Пойманы два преступника (A и B), совместно совершивших одно вооруженное ограбление. Однако, следствие не может доказать, что вооруженное ограбление совершили именно они. Следствие может лишь доказать, что они незаконно носили оружие. По закону за вооруженное ограбление положено тюремное заключение сроком на 10 лет, за ношение оружия – 1 год тюрьмы. В связи со сложившейся ситуацией следователь предлагает каждому участнику сознаться. Также он сообщает, что если сознаются оба участника, то каждому из них срок будет сокращен в два раза до 5-ти лет. Возможности общаться между собой у заключенных нет. Вопрос: следует ли каждому из заключенных сознаться или продолжать молчать?

В данном случае следователь придумал условия «игры». А заключенные A и B играют в нее между собой. Для описания условий игры между двумя игроками и возможных сценариев обычно используется матрица, измерениями которой являются возможные сценарии (выборы) каждого игрока, а в ячейках результат игры в случае данного сочетания выборов двух игроков.

Для краткости и четкости обозначим в ячейках матрицы результаты для игроков A и B в виде: результат А, результат B.

Заключенные хотят получить «гарантированный» оптимальный результат игры при любых стратегиях другого игрока. Для этого, т.к. заключенные не связаны друг с другом, при принятии решения (сознаться или молчать) они рассматривают для каждой возможной стратегии наихудший результат. Так, если заключенный A сознается, то его наихудший результат равен -10 (если B сознается). В случае же, если А будет продолжать молчать, то его наихудший результат равен -1 (если B также будет продолжать молчать). Следовательно, А выбирает для себя стратегию «молчать», как наиболее эффективную при любых действиях B. Нетрудно увидеть, что для B «молчать» — также оптимальная стратегия. В итоге оба заключенных будут молчать и выйдут на свободу через год. Если кто-то из них не владеет аналитическим аппаратом принятия решения, то он в итоге может просидеть в тюрьме 5 или даже 10 лет, за счет чего владеющий им может выйти сразу на свободу.

Но, конечно же, оба заключенных поймут суть сложившейся ситуации и будут молчать. Единственным человеком, не владеющим аппаратом теории игр, был в данном случае следователь, который придумал такие условия игры для подозреваемых, что виновные в серьезном преступлении получат на двоих всего 2 года тюрьмы.

В условиях невозможности доказательства вины ему следовало бы предложить другую игру. А именно, предложить каждому подозреваемому сознаться, но взамен обещать свободу сознавшемуся, если его партнер продолжит молчать, или уменьшение срока вдвое, если его партнер также сознается.

В этом случае матрица результатов для заключенных выглядит следующим образом.

Наихудшие результаты для А при любых действиях B, если сознаться = -5, если молчать = -10. Следовательно, А выгоднее сознаться. Аналогично выгоднее сознаться и B. Следовательно, оба подозреваемых сознаются и получат по 5 лет тюрьмы.

Такой исход хорош для следователя (общества в целом) и плох для криминала. «Профсоюз» криминала в лице мафии во избежание подобных ситуаций может ввести для своих членов правило: «не сознаваться ни при каких условиях». За неисполнение этого правила гарантированная смерть после освобождения из тюрьмы. Пусть нашим заключенным по 30 лет и средняя продолжительность жизни 60 лет, т.е. смерть эквивалентна потере 30 лет жизни.

Матрица тогда выглядит так.

Наихудшие результаты для А при любых действиях B, если сознаться = -30, если молчать = -10. Следовательно, А, как и B, выгоднее молчать. В итоге оба получат всего лишь по году тюрьмы.

Приведенный выше пример показывает возможность применения элементарных инструментов теории игр для принятия решений. Более сложные случаи могут быть смоделированы развитым математическим аппаратом теории игр, в т.ч. при помощи методов линейного программирования рассмотренных выше.

Теория очередей

Очереди – это наше все! Они повсюду. В магазине, в аэропорту на регистрации и оформлении багажа, в самолете при ожидании разрешения на посадку, в автомобиле в пробке и т.д. и т.п. Поэтому, из-за их распространенности и важности, для описания и поддержки принятия решений в сфере «очередей» была создана теория массового обслуживания (теория очередей). Математический аппарат, лежащий в основе теории очередей, весьма и весьма сложен, подразумевает решение системы дифференциальных уравнений большого порядка. Однако, результатом его применения являются несложные формулы, позволяющие рассчитывать характеристики очередей и, тем самым, принимать решения по их оптимальной организации.

Рассмотрим обобщенную модель очереди.

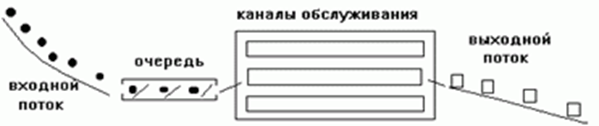
«Входной поток» представляет из себя общий поток заявок желающих получить обслуживание. «Канал обслуживания» обрабатывает не более одной заявки одновременно. Для одновременной обработки N заявок может использоваться N каналов. «Выходной поток» — обработанные заявки. Если интенсивность входного потока (число заявок в единицу времени) превышает число каналов обслуживания, то «не помещающиеся» заявки становятся в «очередь» с тем, чтобы быть обработанными в следующую единицу времени.

Наглядным примером, который может быть описан при помощи данной модели является Call-центр оператора связи. Так абоненты, желающие получить консультацию по телефону, образуют входной поток. Канал обслуживания – оператор. Call-центр — группа операторов, обрабатывающих телефонные звонки. Если в Call-центре есть свободный оператор, то абонент сразу попадает на него, минуя очередь. Если в Call-центре все операторы заняты, то он становится в очередь и слушает музыку в своем телефоне в это время. Размер такой «очереди» в Call-центре имеет свои технологические ограничения и если желающих дозвониться абонентов слишком много, а операторов (каналов обслуживания) слишком мало, то очередь переполняется и никакие другие абоненты просто не могут дозвониться по указанному номеру телефона (слышат короткие гудки «Занято»).

Теория очередей и формулы, приведенные ниже, в частности, позволяют рассчитать необходимое количество операторов и размер очереди для того, чтобы справиться с прогнозируемым количеством звонков абонентов с одной стороны и не переплачивать за релаксирующих операторов с другой стороны.